Fyzikální poradna
Máš nějaký dotaz?
Pokud se chceš na něco zeptat, napiš nám e-mail s předmětem „Fyzikální poradna“ na adresu: poradna@svetenergie.cz
Černobyl
Dobrý den, mám jeden technický dotaz ohledně katastrofy v Černobylské jaderné elektrárně. V poslední době se tato nehoda stala diskutovaným tématem díky úspěšnému televiznímu seriálu a mě by konkrétně ...
Ahoj Ondro,
děkujeme ti za dotaz do naší poradny. Osobně chválím to, že přemýšlíš nad tím, co vidíš a také, že se snažíš najít odpovědi.
V tomto případě budu spíše odhadovat, protože nejsem ani jaderný fyzik, ani znalec reaktorů.
Obecně bych čekal, že jde o bezpečnostní nádrž (např. zde: https://www.physicsforums.com/threads/whats-the-control-system-tank-in-rbmk.971674/) ...
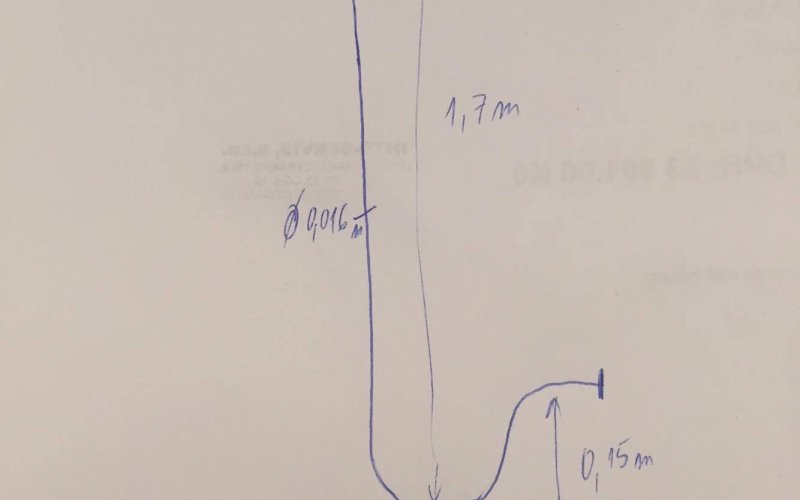
Hadice
Dobrý den, mohl bych Vás poprosit o vysvětlení jevu? Máme hadici na odvod kondenzátu z klimatizace o průměru 16mm vedoucí dle schématu v příloze. Do hadice kape voda po kapkách ...
Zdravím Petře,
vypadá to jako záhada. Ještě mi chybí vědět, kam přesně hadice vytéká – jestli do volného prostoru, nebo do odpadní trubky.
Pokud by kondenzát tekl volně ven, tak buhužel nemám žádné vysvětlení – hydrostatický tlak nijak nesouvisí s tloušťkou hadice ani s rychlostí přítoku kapaliny, takže by voda měla bez problémů odtékat ...
Kolik se při elektrolýze vyrobí vodíku a kolik kyslíku z jednoho litru vody?
Dobrý den, moc rád bych znal odpověď na následující otázky. Kolik se při elektrolýze vyrobí vodíku a kolik kyslíku z jednoho litru vody? Při spálení vodíku v plynovém turbínovém generátoru vznikne něj ...
Ahoj Michaeli,
omlouvám se, ale na tvoje otázky podám jen obecnou odpověď, rád bych se vyhl tomu, aby tato poradna sklouzla do poradny řešení domácích úkolů.
K první otázce - zadání není úplné - není jasné, v jakých jednotkách má být to „kolik“. Pokud jde o litry, tak záleží na okolním tlaku a teplotě (dle stavové rovnice pro ideální plyn) ...
Je v horkovzdušné a parní troubě, kde na boku stěny je odštípnutý smalt o velikosti 2 cm, zdravotně nezávadné péct a připravovat jídla v páře?
Dobrý den, je v horkovzdušné a parní troubě, kde na boku stěny je odštípnutý smalt o velikosti 2 cm, zdravotně nezávadnéné péct a připravovat jídla v páře? Jídlo není s poškozeným smaltem v kontaktu, ...
Dobrý den,
děkujeme za praktickou otázku do naší snad praktické fyzikální odpovědny. Z toho, kolikrát jsem použil slovo praktický, je doufám vidět, že se považuji za praktického člověka. Tak se budu snažit i odpovědět, ale berte, prosím v potaz, že tato odpověď není nijak věděcká, neb nejsem odborník ani na vaření, ani na vliv materiálů na zdraví člověka ...
Černobyl
Dobrý den, i já bych měl jeden dotaz ohledně katastrofy v Černobylu. Prakticky velké množství článků, které lze o této katastrofě nalézti popisuje událost jako dva zásadní výbuchy, kde první výbuch zp ...
Dobrý den Jaroslave,
po pravdě se obávám, že na danou otázku jste asi větší odborník Vy. Obecně se nepovažuji za příznivce konspiračních teorií a (možná bláhově) důvěřuji oficiálním zdrojům – tedy v demokratických zemích.
Domnívám se, že samotná havárie v Černobylu byla důkladně a opakovaně prošetřena nezávislými organizacemi a jejich zjištění potvrzuje, že došlo k výbuchu páry a vodíku ...
Pád tělesa z výšky
Dobrý deň. Chcem sa spýtať, ak máte dve rovnaké telesá, ktoré majú rovnakú hmotnosť a budú padať z rovnakej výšky, majú však rôzny tvar. Dopadnú rovnako? Ďakujem
Dobrý den,
na podobný dotaz jsem zde již odpovídal (www.svetenergie.cz/cz/fyzikalni-poradna…), proto si dovolím být stručný.
Na takto položený dotaz lze odpovědět vždy správně, protože nebylo řečeno v jakém prostředí k volnému pádu dochází.
Pokud bude k pádu docházet ve vakuu, nemá na pohyb těles vliv ani jejich hmotnost, ani jejich tvar (a vlastně žádná jiná vlastnost tělesa) ...
Seskok parašutisty
Dobrý den, měl jsem s kolegou „fyzikální spor“. Jde o seskok parašutisty. Tvrdil jsem, že seskok parašutisty je po celou dobu volný pád (tedy i po otevření padáku) a to za podmínky, že zanedbáváme odp ...
Dobrý den,
děkujeme za další dotaz do naší poradny, těší mě vaše důvěra a budu se snažit váš kolegiální spor vyřešit.
Pokud bychom brali pohyb parašutisty bez odporu vzduchu (tedy ve vakuu), tak správně odhadujete, že jde o volný pád. Jenže v tu chvíli nebude mít otevření padáku na pohyb parašutisty jakýkoliv vliv – nebude žádné okolní prostředí, které by na padák působilo ...
Bazén na měsíci
Je známá věc, že na Měsíci má člověk zhruba šestkrát menší tíhu než na Zemi. A teď si představte, že byl na Měsíci vybudován bazén a chcete se v něm vykoupat ...
Ahoj Pavle,
děkujeme za dotaz do naší poradny. Ze začátku Tě musím pochválit za správnou terminologii – je to jak píšeš, tíha čehokoliv je na Měsíci (zhruba) 6x menší. Hmotnost je stále stejná. Zároveň jsi si vlastně odpověděl na svou otázku ...
Podtlak v cisterně
Dobrý den, dočetl jsem se o metodě čerpání (fekálií), kdy se v cisterně odpálila dávka benzínu a vznikl tak podtlak. Není mi jasné, jak přesně to mohlo fungovat ...
Ahoj Libore,
děkujeme za sice ne moc voňavý, ale praktický dotaz do naší poradny. Sice jsem nic podobného neslyšel, ale v principu to možné je. Vlastně je to stejné, jako pokus se svíčkou. Zapálením benzinu se zvýší teplota v cisterně. Při zvýšení teploty se začne vzduch v cisterně teplotní roztažností rozpínat. Pokud nebude mít kam unikat, tak vznikne v nádobě přetlak ...
Elektrický spotřebič ve vaně
Už delší dobu řeším problém: Často vidíme ve filmech, že se někdo koupe ve vaně a jiný do vody hodí nějaký zapnutý el. spotřebič a koupající se osoba zemře ...
Ahoj Štěpáne,
doufám, že tento problém řešíš pouze v teoretické rovině.
Pokus, který popisuješ byl nejspíše proveden s destilovanou vodou – ta neobsahuje ionty, což jsou volně pohyblivé nabité částice. Podmínkou vedení el. proudu je to, že materiál, kterým chceme el. proud vést obsahuje volně pohyblivé nabité částice. V kovech jsou to typicky volné elektrony, v kapalinách a plynech ionty ...
Ohřej si vodu, ať ti zmrzne rychleji …
Vážený pane doktore, v návaznosti na předchozí dotaz prosím o vysvětlení následujícího jevu: Když necháte na mrazu dvě identické nádoby jednu se studenou a druhou s horkou vodou, zamrzne dříve ta hork ...
Dobrý den,
děkuji za pozornost, kterou věnujete naší poradně a za navazující dotaz.
To, co popisujete, se nazývá Mpembův jev. Erasto Mpemba si všiml toho, že v mrazáku zamrzne teplá voda rychleji, než studená. Ale je důležité si uvědomit, že to není pravidlo – tato situace nastává jen někdy, obecně lze říci, že čím větší mrazák, tím spíše k rychlejšímu zrznutí horké vody dojde ...
Prázdnou láhev plnou nenaplníš …
Dobrý den, rád bych se zeptal na následující věc. Mám dvě 8litrové tlakové lahve na CO2. Jedna je plná a druhá je úplně prázdná ...
Ahoj Pavle,
děkujeme za dotaz do naší poradny, nejsi jediný, kdo podobný problém řeší – před půl rokem jsem stejnou otázku řešil s kamarádem. Ten na problém šel od konce – nejdřív to zkusil a pak zjišťoval, proč to nejde. Takže jsem vlastně odpověděl na tvůj dotaz – nic (výrazného) se dít nebude. Další otázkou je proč tomu tak bude ...
Výroba ultrazvukové čističky
Dobrý den, přemýšlím o vyrobení ultrazvukové čističky. Dotaz je, zda lze k tomu využít ultrazvuková píšťalka na psy? Jako pohon kompresor, nebo vzduchovací motorek do akvária ...
Ahoj Honzo,
děkujeme za otázku do naší poradny, ale bohužel tě budu muset zklamat. Nepůjde to.
Ultrazvukové píšťalky na psy mají frekvenci do cca 35 kHz (to je frekvence, kterou psi ještě vnímají), kdežto ultrazvukové čističky pracují na vyšších frekvencích. To je první a nejjednodušší důvod, proč to nepůjde. Druhý spočívá v tom, v jakém prostředí se píšťalka používá – to je vzduch ...
zkrat v televizi
Dobrý den, chtěl bych vás požádat o odbornou radu a předem děkuji za odpověď. Před několika dny v našem městě došlo k výpadkům proudu, který se opakoval asi 20x během cca třech hodin ...
Dobrý den Miroslave,
děkujeme za dotaz do naší odpovědny, myslím, že nejste sám, komu se něco podobného stalo.
Nejdříve bych se věnoval zkratu „základní desky“. Elektronika se dnes obvykle vyrábí tak, že velké množství součástek je integrováno na plošném spoji. To je možné díky tomu, že jsme schopni dříve velké součástky nahradit polovodičovými, které dokážeme výrazně miniaturizovat ...
Vnímání času
Dobrý den, měl bych prosbu o vysvětlení mé myšlenky. Lidské oko má nějaké FPS které dokáže postřehnout, podle internetu je to od 24 fps pro lidské oko plynulý obraz ...
Ahoj Ondro,
děkujeme za dotaz z pomezí biologie a fyziky. Vždy mě potěší, když lidé přemýšlejí nad světem kolem sebe a nad různými souvislostmi. A pak mě potěší, že vše jde vysvětlit jednoduše a i s využitím pojmů, které nám mohou přijít nezajímavé.
Při vysvětlení si vystačíme se základními jednotkami a jejich definicemi. Určitě jsi se je učil, stejně jako další naši čtenáři ...
Proč jedno těleso natáhne pružinu více než druhé?
Dobrý den, řešíme s přáteli jednoduchý příklad, ve kterém jsou na pružinách zavěšena dvě různě hmotná tělesa ...
Jane, dobrý den, děkuji za novou otázku do naší poradny.Popravdě nemám moc, co bych na vašem dotazu opravil či dovysvětlil. Je pravda, že ve fyzice si často pomáháme zjednodušeními, ale nemělo by to být na úkor pochopení principu ...
Čas – Prostor – Entropie – Kodaňská interpretace
Dobrý den, pokusím se to shrnout co možná nejstručněji – předem upozorňuji, že nejsem žádný odborník / expert na fyziku a se středoškolskou látkou jsem docela zápasil, nicméně některá témata, např ...
Ahoj Jakube,
děkujeme za otázky do naší odpovědny a já osobně děkuji za důvěru, kterou ve mě vkládáš. Pokusím se odpovědět v rámci svých znalostí, ale jako obvykle půjde o zjednodušení a také musím upozornit, že jsem jen středoškolský učitel, takže se nepovažuji za odborníka na kvantovou fyziku a fyziku mikrosvěta ...
Jak padají tělesa ve vzduchoprázdnu a jak ve vzduchu?
Dobrý den, ráda bych Vás požádala o radu na internetu jsem na vás narazila náhodou a tak vás chci požádat o radu. Můžete mi pomoci s otázkou, Jak padají tělesa ve vzduchoprázdnu a jak ve vzduchu ...
Ahoj,
omlouvám se, ale nejsem si přesně jistý, jakým směrem se mám ve tvé otázce ubírat. Zkusím odhadnout co přesně tě zajímá, pokud bych se netrefil, zkus svůj dotaz upřesnit.
Pokud bych se zaměřil na to, jaký vliv má vzduch (nebo jiné prostředí) na volný pád těles, tak je odpověď vcelku jednoduchá, myslím, že jsme se tomu v poradně i několikrát věnovali ...
Kolik se odpaří vody z horní nádrže elektrárny Dlouhé stráně?
Dobrý den, mám dotaz potřeboval bych nějaký zjednodušený výpočet kolik se odpaří vody z horní nádrže elektrárny Dlouhé stráně ...
Dobrý den,
děkujeme za další dotaz do naší poradny, tentokrát je vlastně i s odpovědí. Určitě si netroufnu jakkoliv rozporovat tvrzení pana Feynmana, naopak si dovolím čtenáře navést k četbě jeho knih, považuji jej za nejen výborného fyzika, ale hlavně za výborného popularizátora vědy a zajímavého člověka.
Pokud bych se zaměřil na početní stránku dotazu, nevidím v ní chybu ...
Teslovy cívky
Cose stane, když se dotknou Teslovy cívky?
Ahoj Tondo, nejspíš myslíš Teslův transformátor - ten se skládá ze dvou cívek. Jako každý transformátor má dvě vinutí (tedy cívky) a poměr závitů na obou vinutích udává, jak se bude měnit napětí a proud na druhé (výstupní, odborně sekundární) cívce ...